Вогнутая линза: что это такое, формулы, применение

Автор:

Вогнутая линза — это линза, которая обладает хотя бы одной поверхностью, чья кривизна направлена внутрь.

Линзы, с которыми мы сталкиваемся в окружающем нас мире, имеют разную форму. Как эти формы влияют на функции линз? Какую роль играют вогнутые линзы (рис. 1.) и для чего они используются? Об этом я расскажу в данной статье.

Вогнутые линзы в фотообъективах
Рис. 1. Вогнутые линзы в фотообъективах

Линзы делятся на:

  • выпуклые;
  • вогнутые.

Вогнутые линзы, в свою очередь, делятся на:

  • a) двояковогнутые — окаймленные с обеих сторон вогнутой сферической поверхностью (рис. 2a);
  • б) плоско-вогнутые — граничат с одной стороны с плоской поверхностью, а с другой стороны с вогнутой сферической поверхностью (рис. 2b);
  • в) выпукло-вогнутые — ограниченные с одной стороны выпуклой сферической поверхностью, а с другой — вогнутой сферической поверхностью (рис. 2c).
Типы вогнутых линз
Рис. 2. Типы вогнутых линз

Оптическая сила линзы зависит от радиусов кривизны двух поверхностей, а также от показателей преломления материала линзы и среды, в которой она находится. Эта взаимосвязь описывается формулой:

D = 1 / f = ( n2 / n1 — 1 ) * (1 / R1 + 1 / R2), где:

  • D — оптическая сила линзы (от англ. optical power). Это физическая величина, равная обратной величине фокусного расстояния линзы (f). Его единица измерения — диоптрия, которая является обратной величиной метра;
  • f — фокусное расстояние линзы;
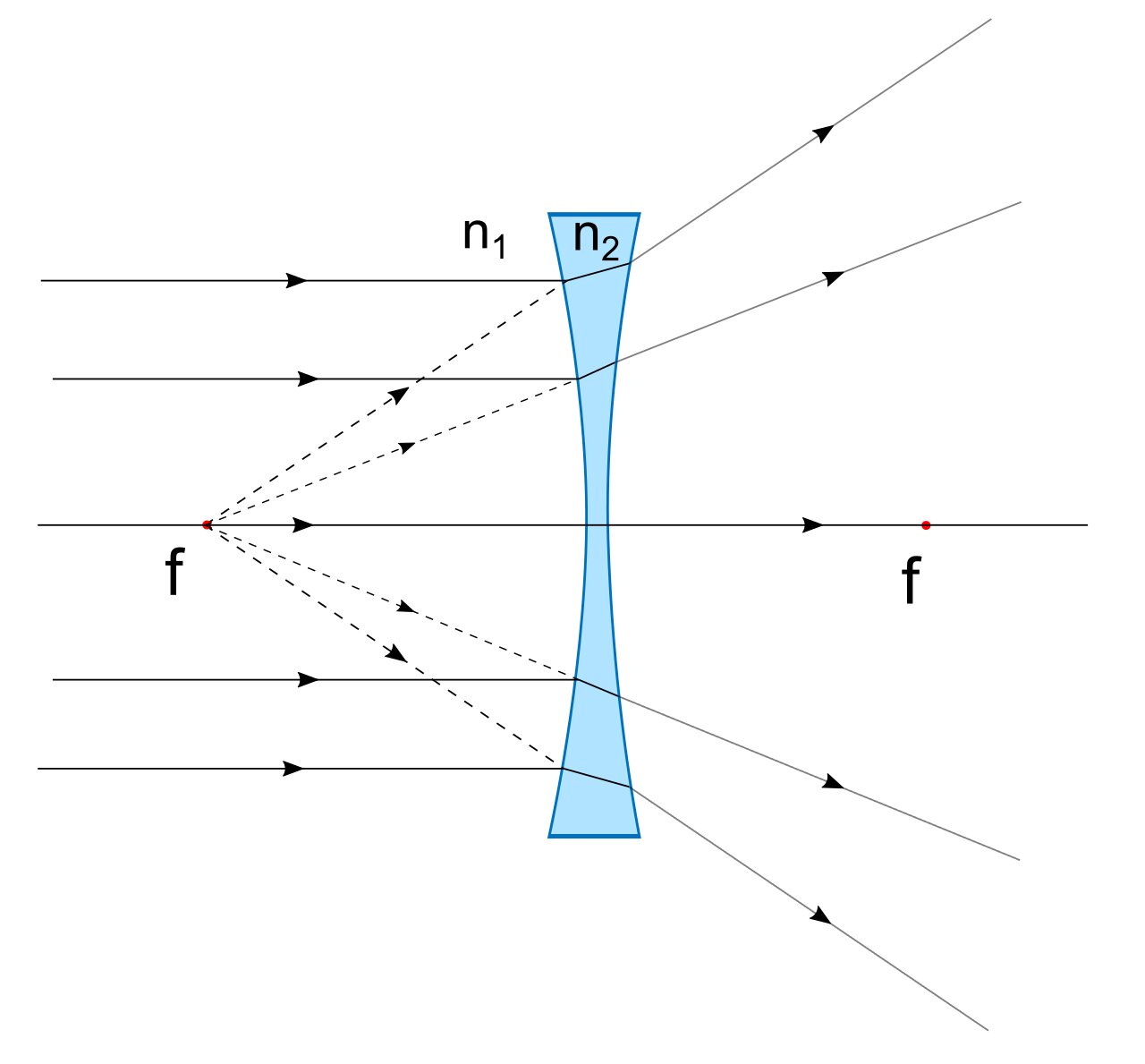
  • n2 — показатель преломления материала, из которого изготовлена рассматриваемая линза;
  • n1 — показатель преломления среды, в которой находится рассматриваемая линза;
  • R1 и R2 — радиусы кривизны линз [м].

В случае вогнутых линз, показанных выше, второй множитель в формуле (1) содержит радиусы кривизны: (1 / R1 + 1 / R2), которые должны принимать следующие значения:

  • для двояковыпуклой линзы (рис. 3): R1 < 0 и R2 < 0, поэтому -1 / R1 — 1 / R2 < 0 ;
Путь лучей в двояковыпуклой линзе
Рис. 3. Путь лучей в двояковыпуклой линзе
  • для плоско-вогнутой линзы (рис. 4): R1 → ∞ и R2 < 0, тогда 1 / R1 — 1 / R2 = 0 — 1 / R2 = — 1 / R2 < 0
Путь лучей для плосковыпуклой линзы
Рис. 4. Путь лучей для плосковыпуклой линзы
  • для вогнуто-выпуклой линзы (рис. 5): R1 < 0 и R2 > 0, тогда -1/R1 + 1/R2 < 0, где 1 / R2 < 1 / R1 и R1 < R2 .
Путь лучей для вогнуто-выпуклой линзы
Рис. 5. Путь лучей для вогнуто-выпуклой линзы

Помимо радиусов кривизны, оптическая сила линзы зависит от ее показателя преломления. Классические линзы для очков, например, имеют показатель преломления примерно 1,5. Если такая линза находится в воздухе, то:

  • для двояковыпуклой линзы выражение (1) отрицательно, поэтому линза является рассеивающей;
  • для плосковыпуклой линзы выражение также отрицательно, так что линза является рассеивающей;
  • для вогнуто-выпуклой линзы в случае, когда R1 < R2 , линза является рассеивающей, а когда R1 > R2 — собирающей.

Однако следует помнить, что одна и та же линза в среде с показателем преломления, превышающим ее собственный, изменяет свою оптическую силу. Таким образом, линза, которая является рассеивающей линзой в воздухе, может стать собирающей линзой при погружении в соответствующую жидкость.

Применение

Приведу несколько распространённых применений линз.

Вогнутые линзы в целом используют в объективах фотоаппаратов, в телескопах и микроскопах.

Двояковогнутые (рассеивающие) линзы используются в корригирующих очках для коррекции близорукости. Считается, что Николай Кузанский был первым, кто открыл преимущества вогнутых линз в лечении близорукости в 1451 году.

Лупа — это пример собирающей линзы, используемой для прямого наблюдения небольших близких объектов. В строгом смысле слова это собирающая линза, дающая как минимум трехкратное увеличение. Линзы, дающие увеличение менее чем в три раза, называются лупами.

Вспомогательные линзы, представляющие собой элементы, установленные на передней части объектива и изменяющие его характеристики, также являются примерами собирающих линз. Например, объектив +4 D имеет фокусное расстояние 25 см, а +1 D = 100 см. Знак плюс указывает на фокусировку, а знак минус — на рассеивание.