Любая электрическая цепь включает в себя ряд элементов, среди которых встречаются активные и реактивные составляющие. При параллельном соединении активного, емкостного и индуктивного элемента схема выглядит таким образом:
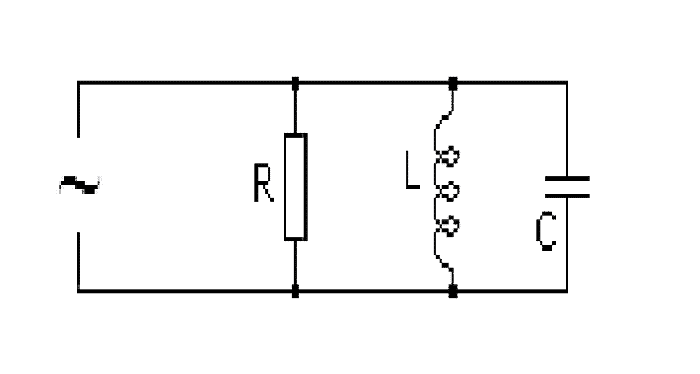
В зависимости от конкретной ситуации тот или иной элемент может исключаться из цепи, меняя тем самым характер нагрузки. Для геометрического определения суммарного значения всех сопротивлений производится сложение векторов. В зависимости от типа реактивной нагрузки результирующий вектор импеданса будет смещаться в положительный или отрицательный квадрант.
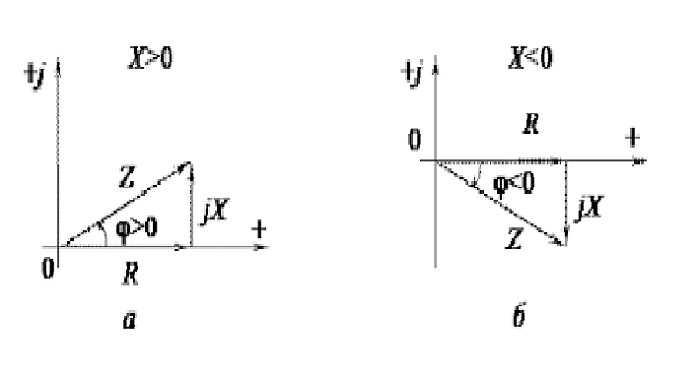
Для вычисления полного сопротивления Z составляется уравнение согласно теоремы пифагора. Только сложению подлежит не сопротивление, а проводимость цепи. Из-за чего уравнение для определения сопротивления можно будет выразить по следующей формуле:
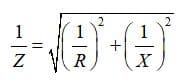
Где Z – комплексное сопротивление участка, R – активное сопротивление участка, X – реактивное сопротивление участка.
При этом реактивное сопротивление выражается как геометрическая сумма проводимости катушки и конденсатора.
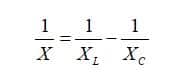
А отдельно расчет XL и XC при известных параметрах сети, емкости и индуктивности самих элементов выполняется по таким формулам:
XL = w * L = 2 * π * f * L,
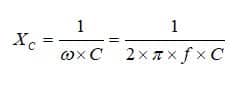
Для определения углов δ и φ необходимо применить тригонометрические функции к отношению соответствующих проводимостей или сопротивлений.
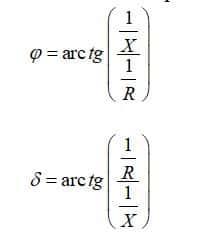
В связи с большим количеством расчетов, применяемых формул и необходимостью использования тригонометрических функций определение импеданса в параллельной цепи является достаточно сложной задачей, особенно, если делать это вручную. Но, при использовании онлайн калькулятора для расчета комплексного сопротивления достаточно ввести частоту, емкость конденсатора, индуктивность катушки и омическое сопротивление резистора. А все расчеты система произведет самостоятельно.
