Выпуклое зеркало — это зеркало, отражающая поверхность которого является внешней поверхностью сферы.
Применение.
Управляя автомобилем, водитель не может представить себе отсутствие зеркал. Без них безопасность движения значительно снизилась бы. Боковые зеркала (рис. 1а) позволяют видеть позади автомобиля, что облегчает движение задним ходом или смену полосы движения.
В местах с ограниченной видимостью (например, на перекрестках или выездах с территории) водитель использует выпуклые зеркала (рис. 1б). Однако выпуклое зеркало не дает реалистичной оценки расстояния. По этой причине, а также по многим другим, стоит ознакомиться с теоретической основой вопроса, описанного в данной статье. Это «облегчит жизнь» в современном мире и позволит избежать многих проблем.

Изучив представленную информацию, вы начнете понимать применение выпуклого зеркала в окружающем мире и описывать получаемые в нем изображения.
Характеристики, описывающие выпуклое сферическое зеркало
Как получить выпуклое зеркало?
Чтобы получить сферическое зеркало, нужно взять сферу, то есть поверхность сферы, и отрезать от нее фрагмент. Затем полученную сферическую часть следует покрыть отражающим слоем (рис. 2). Придав зеркальный блеск его внешней стороне, мы получим выпуклое сферическое зеркало.

Параллельные лучи, падающие на сформированное таким образом зеркало, после отражения от его поверхности не пересекаются в одной точке, а образуют расходящийся пучок — как показано на рис. 3 (чтобы избежать сферической аберрации, мы рассматриваем осевые лучи, то есть те, которые лежат вблизи оптической оси системы).
Однако, нарисовав продолжения этих лучей, мы увидим, что они пересекаются по другую сторону зеркала — в точке, которую мы называем фокусной и обозначаем буквой F. Если поместить в эту точку экран, изображение предмета на нем не появится — следовательно, фокус имеет другую природу, чем в случае вогнутого сферического зеркала — он мнимый (кажущийся). Расстояние между фокусной точкой и зеркалом называется фокусным расстоянием и обозначается буквой f.
Связь между радиусом кривизны зеркала (т.е. радиусом сферы, из которой образовано зеркало) и фокусным расстоянием выражается формулой: f = r / 2, где:
f — фокусное расстояние [м];
r — радиус кривизны зеркала [м].

Формирование и построение изображений в выпуклых зеркалах
Для построения изображения, создаваемого выпуклым сферическим зеркалом, как и в случае с вогнутым сферическим зеркалом, мы используем два луча, отраженных от его поверхности. В точке пересечения их продолжений мы получим искомое изображение. Здесь могут быть использованы следующие лучи:
- Луч, параллельный оптической оси, который отражается от зеркала таким образом, что его продолжение проходит через фокус этого зеркала (рис. 4. — луч 1).
- Луч, падающий на вершину W зеркала под любым углом α, отражается под тем же углом α (рис. 4. — луч 2).
- Луч, падающий на поверхность зеркала под углом 0° (продолжение которого проходит через точку O, центр кривизны зеркала), отражается под тем же углом 0°, поэтому путь отраженного луча такой же, как у падающего (рис. 4. — луч 3).

Кроме того, для характеристики изображений, получаемых в зеркале, используются следующие понятия: расстояние объекта изображения от отражающей поверхности x и расстояние изображения от зеркала y. Для выпуклого сферического зеркала справедливо уравнение зеркала: 1 / f = 1 / x + 1 / y , где:
- f — фокусное расстояние [м];
- x — расстояние объекта от зеркала [м];
- y — расстояние изображения от зеркала [м].
При применении уравнения зеркала необходимо учитывать знаки отдельных величин. Если предположить, что лучи света падают на зеркало слева направо, тогда стоит считать, что слева от отражающей поверхности (то есть в направлении лучей) — величины будут иметь знак «+», а справа от этой поверхности — знак «-«. Поэтому в случае выпуклого сферического зеркала и радиус кривизны зеркала, и фокусное расстояние отрицательны.
Рассмотрим далее, как можно описать зависимость y от x. Преобразуя вышеприведенное уравнение, получаем: y = f / (1 — f / x).
Представим это на графике y(x) (см. рисунок 5):
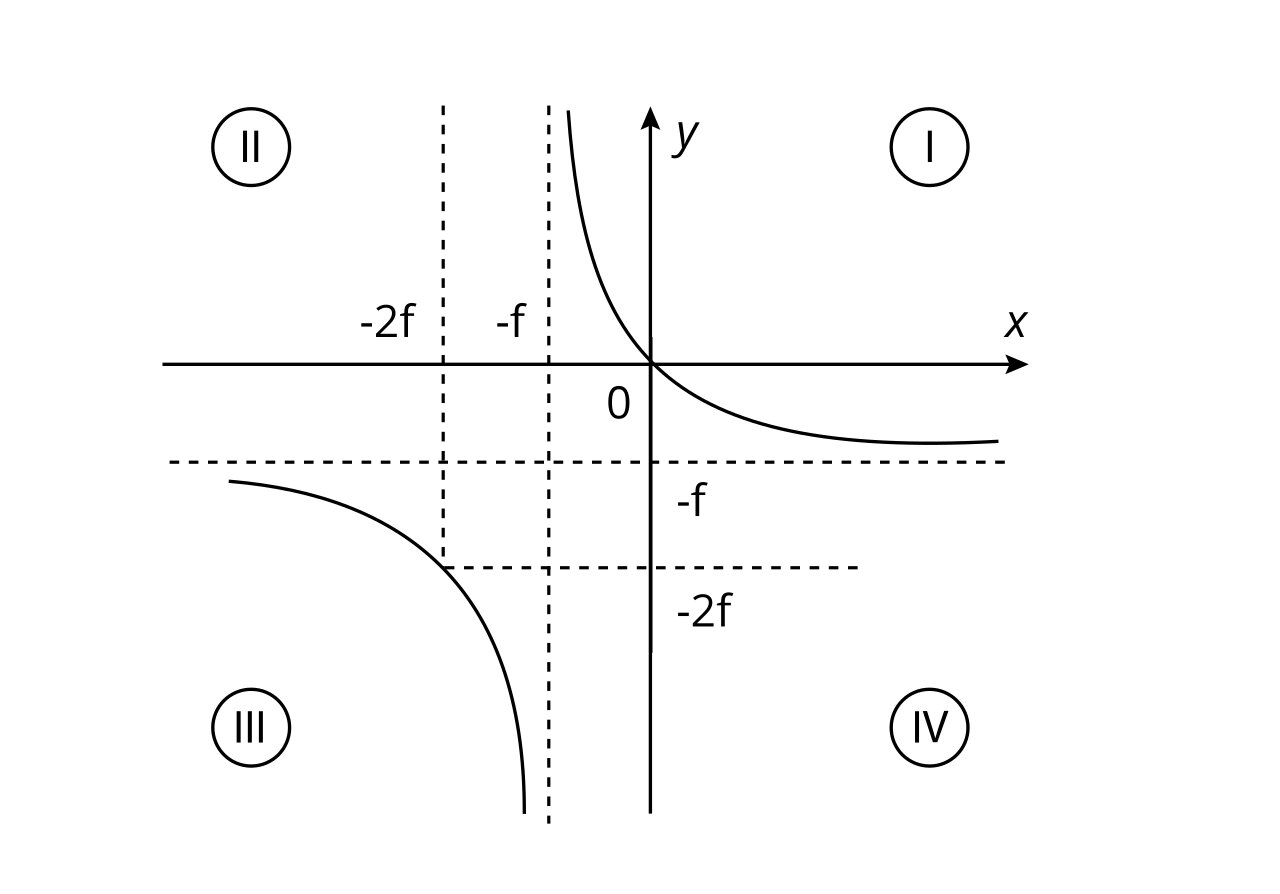
Рассмотрим график y(x) (рис. 5). В зависимости от расстояния объекта от зеркала можно заметить, что формируемое в нем изображение выглядит следующим образом:
- x > 0
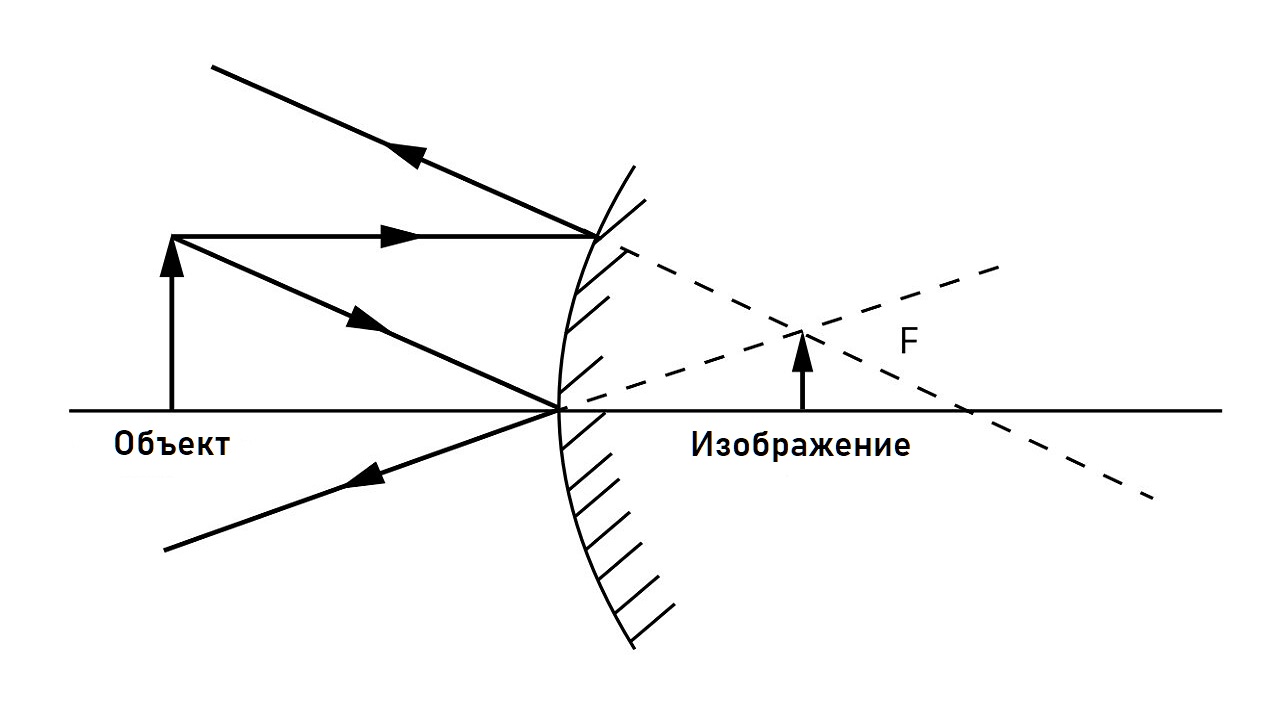
При x > 0 между отражающей поверхностью и фокусом всегда формируется изображение. Это мнимый, прямой и уменьшенный образ.
Сходящийся луч также может быть направлен на выпуклое зеркало. Это означает, что в точке пересечения лучей должно появиться действительное (реальное) изображение, но этого не происходит, потому что лучи отражаются. Тогда мы говорим о мнимом объекте. Лучи, отраженные от зеркала, пересекаются, давая действительное изображение (рис. 7.). Используя правило о знаках величин, запишем: f < 0, x < 0 и y > 0.
- f < x < 0
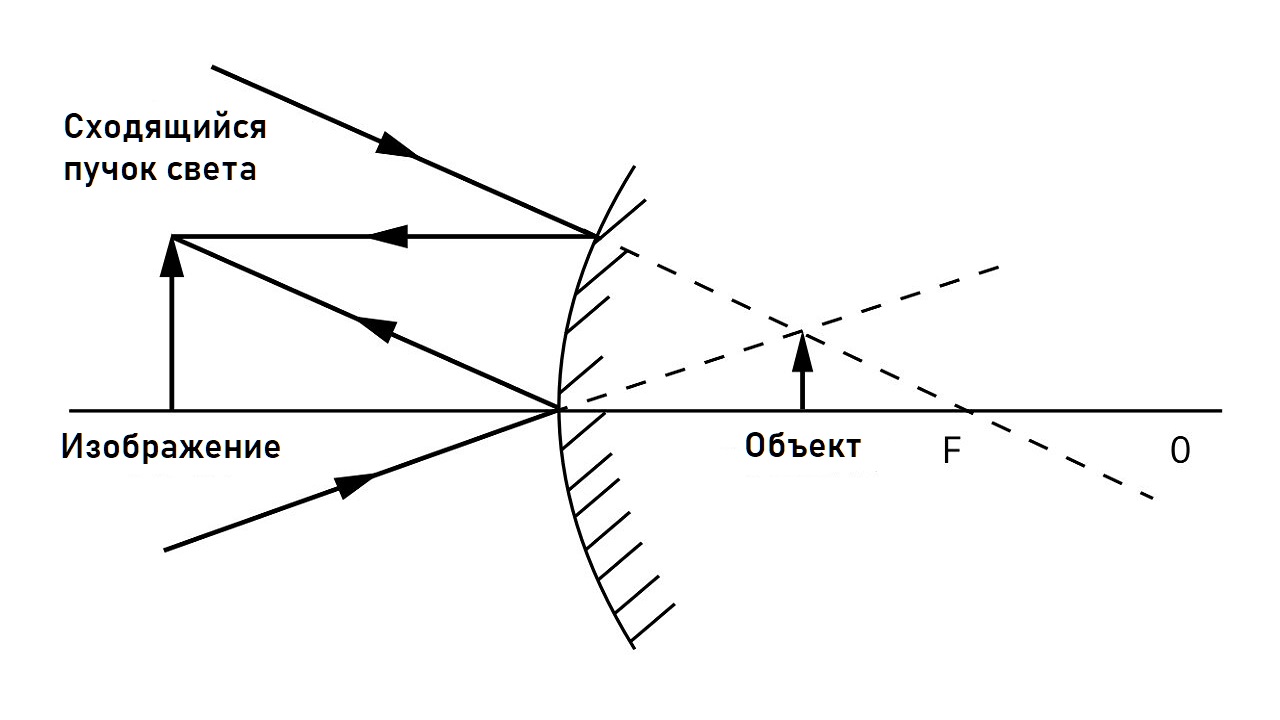
Для 0 > x > f мнимый объект дает нам действительное изображение.

Для x > 0 и |x| > |f| мнимый объект дает нам мнимое изображение.
Линейное увеличение.
Кроме того, при описании изображений, формируемых в выпуклых сферических зеркалах, вводится понятие линейного увеличения p. Это отношение линейных размеров изображения ho и объекта hp: p = ho / hp .
Линейное увеличение (от англ. linear magnification) — это безразмерная величина, представляющая собой отношение линейных размеров изображения ho и объекта hp. Его также можно записать как абсолютное значение от отношения расстояния между изображением и объектов и зеркалом, то есть p = | y / x | .
Википедия
Почему мы используем здесь модуль от деления y на x? Мы используем его, потому что величины x и y могут принимать отрицательные значения. С другой стороны, отношение двух высот ho и hp не может быть меньше нуля.
При p > 1 мы получаем увеличенное изображение, при p < 1 — уменьшенное, а при p = 1 изображение будет иметь тот же линейный размер, что и объект.
Выпуклое сферическое зеркало позволяет, в частности, увеличить поле зрения. Таким образом, изображение смещается ближе к поверхности зеркала и становится меньше (по сравнению с изображением, создаваемым плоским зеркалом). Кажется, что объект находится гораздо дальше, чем на самом деле. Это не позволяет реально оценить расстояние.
